|
To calculate the size of the Power Factor Correction you need
|
|
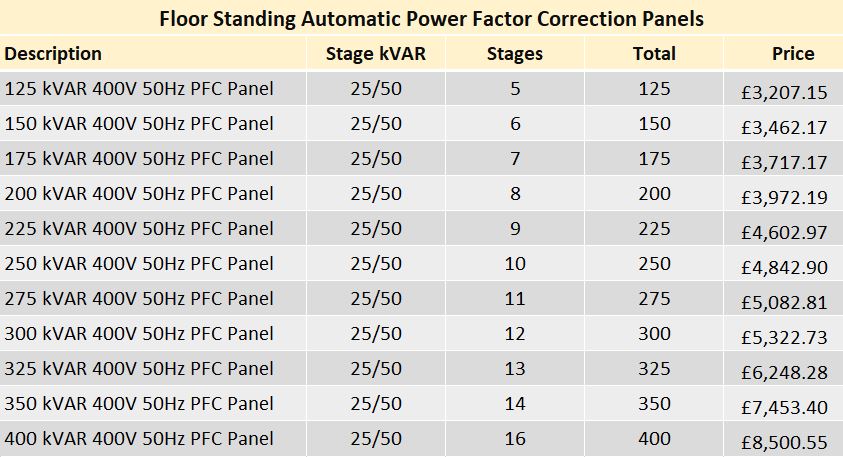
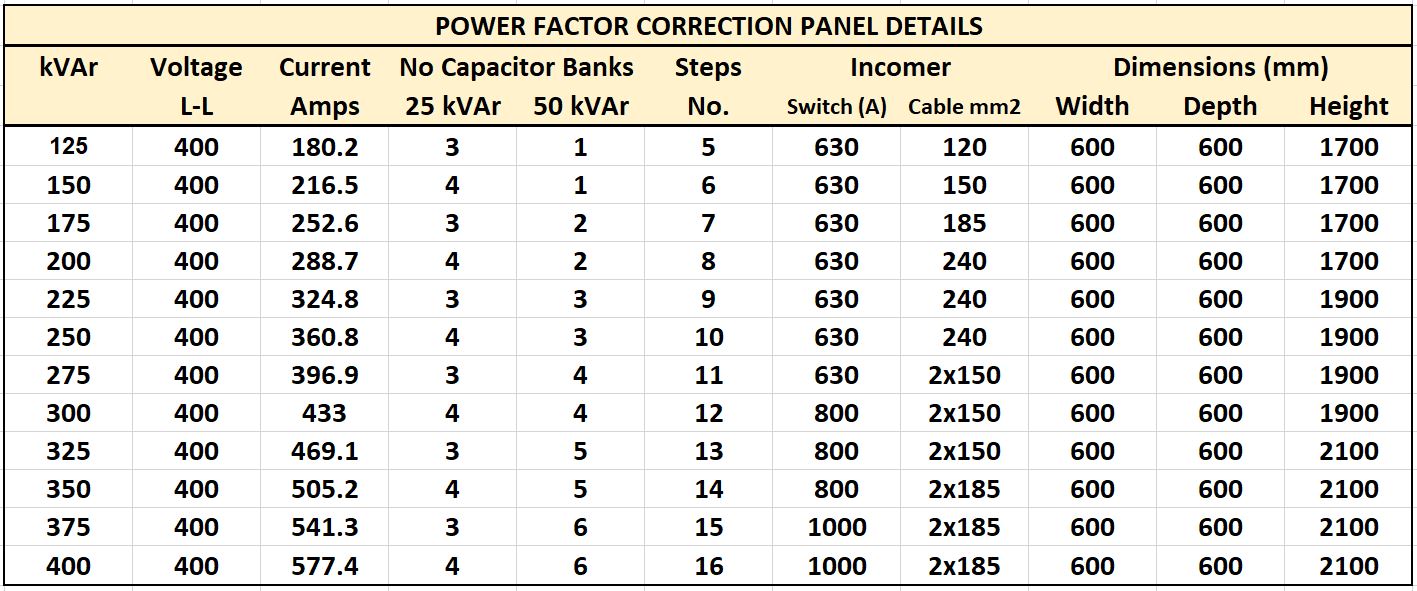
Rating - 125 kVAr - £2,995,00 excl VAT
4 Stages - 1 x 50kVAr - 3 x 25 kVAr Automatic Controller Incoming 250A TP MCCB Part No - MSPFC1253S Dims (mm)- 1700H x 600W x 600D |
Rating - 150 kVAr - £3,295,00 excl VAT
5 Stages - 1 x 50kVAr - 4 x 25 kVAr Automatic Controller Incoming 400A TP MCCB Part No - MSPFC1503S Dims (mm)- 1700H x 600W x 600D |
Rating - 200 kVAr - £3,795,00 excl VAT
6 Stages - 2 x 50kVAr - 4 x 25 kVAr Automatic Controller Incoming 630A TP MCCB Part No - MSPFC2003S Dims (mm)- 1700H x 600W x 600D |
|
Prices exclude VAT. For De-Tuned models please contact us.
|
INTRODUCTION
Correct design of electrical installations and service equipments permits reducing waste, but above all a rational use of the electrical energy with ensuing optimisation of the correlated costs.
A fundamental characteristic of minimizing expenses related to the purchase of energy is to reduce losses, starting from generation and on to distribution and use.
Power-factor correction is one of the actions that make it possible to accomplish
substantial energy savings as it:
POWER FACTOR
Much electrical equipment (especially in the industrial field, such as for example motors, transformers, reactors or power converters), in addition to power known as “active power” (P) capable of translating into work of a mechanical nature, heat,light, etc., needs power known as “reactive power” (Q) needed to energize magnetic circuits.
In other words, we can affirm that not all the energy is used to do work, but only the portion relating to active power.
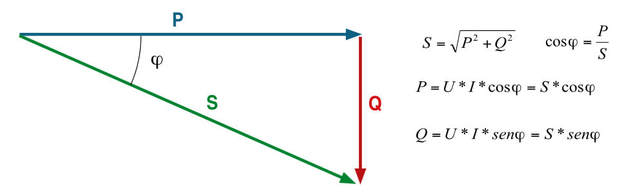
Electric installations must however be designed by taking into consideration power known as “apparent power” (S), given by the product of voltage and current. To clarify matters, it is possible to consider the total current to which the apparent power is associated as the vectorial sum of a resistive component IR (component in phase with the voltage due to the resistive portion of the load), to which the active power P is associated, and the inductive current IL (wattless component due to the inductive portion of the load), to which the reactive power Q is associated.
The apparent power S therefore takes account of both the active power P and the
reactive power Q. Figure A shows the relationship between active, reactive and apparent power by means of the so-called “power triangle.”
The relationship between the active power P and the apparent power S is called the
power factor and is usually indicated as “cos φ”.
Correct design of electrical installations and service equipments permits reducing waste, but above all a rational use of the electrical energy with ensuing optimisation of the correlated costs.
A fundamental characteristic of minimizing expenses related to the purchase of energy is to reduce losses, starting from generation and on to distribution and use.
Power-factor correction is one of the actions that make it possible to accomplish
substantial energy savings as it:
- limits energy losses due to the Joule effect along the cables
- limits drops in voltage along the cables
- reduces plant engineering costs for users, making it possible to utilize conductors with a smaller cross-section
- prevents users from incurring the penalties contained in electrical energy supply contracts.
POWER FACTOR
Much electrical equipment (especially in the industrial field, such as for example motors, transformers, reactors or power converters), in addition to power known as “active power” (P) capable of translating into work of a mechanical nature, heat,light, etc., needs power known as “reactive power” (Q) needed to energize magnetic circuits.
In other words, we can affirm that not all the energy is used to do work, but only the portion relating to active power.
Electric installations must however be designed by taking into consideration power known as “apparent power” (S), given by the product of voltage and current. To clarify matters, it is possible to consider the total current to which the apparent power is associated as the vectorial sum of a resistive component IR (component in phase with the voltage due to the resistive portion of the load), to which the active power P is associated, and the inductive current IL (wattless component due to the inductive portion of the load), to which the reactive power Q is associated.
The apparent power S therefore takes account of both the active power P and the
reactive power Q. Figure A shows the relationship between active, reactive and apparent power by means of the so-called “power triangle.”
The relationship between the active power P and the apparent power S is called the
power factor and is usually indicated as “cos φ”.